There are two alternative implementation methods for this variant. The algorithm optimized in terms of computing time is based on the calculation as explained by Spiess & Florian in 1989. This algorithm allows only simple coordinations and additive fares to be taken into consideration. The alternative approach allows for additional choice model settings and more complex definitions in terms of coordinations and fares.
If the passenger does not have additional information, he has to decide ad hoc whether to board the arriving line or not. The choice model determines the optimal set of lines, and the optimal strategy of the passenger is to choose the line in the set that arrives first.
In addition to the missing passenger information, the model introduced in this section is most notably characterized by the fact that the headway (the temporal gap between two departures of a line) is not assumed to be a constant, but rather exponentially distributed. The expected gap value is exactly the same as for constant headways 1 / λi, therefore the "Frequency" of the line. In contrast to constant headways, however, the headway times strongly scatter around this value.
Fundamental characteristic of the exponential distribution which is taken as a basis is that the wait time which has already elapsed since the last departure of the line, does not state how long the passengers have to wait for the next departure. This property is called "Memorylessness". Thus, the greatest possible irregularity of the timetable is assumed.
The optimal set under these model assumptions is composed as follows. The following is set first:
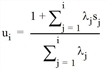
Then, the optimal set of lines is achieved by L* = Li*, where i* = max{i:si≤ ui-1}.
It can be proved that the i* composed in such a way reduces the expected remaining costs.
A line i thus exactly belongs to the optimal set if its remaining travel time (without wait time) is not higher than the expected remaining travel time plus wait time of the combined lines Li-1 = {1, ..., i-1}. This procedure has the effect, that comparatively few lines are used, because with this comparison the lines Li-1 are treated in such a way, as if they were perfectly coordinated. Coordinated here means, that they are arranged so evenly, that they appear as a single line with frequency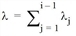 
. Such an additivity is only given in the case of exponential distribution.
The share of the lines i ∈ L* are equal to the probability, that they depart first, as can be taken from the following formula.
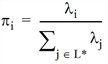
Note, that the remaining travel times of the lines do not appear in the share definition. If lines are adequate enough to be contained in the optimal line set, their shares only depend on their headways. This property illustrates the heavily simplified construction of this choice model.
The resulting expected wait time is as follows.
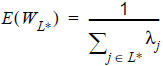
This choice model should only be used if the line headways are extremely irregular, in other words, if the passengers face a high level of uncertainty.
